Manacher算法原理详解以及代码实现
简介
Manacher(马拉车)算法是一个求解字符串最长回文子串的高效算法,可以达到O(n)的时间复杂度
Manacher算法的核心在于:
-
1.通过动态规划的思想,使用数组r,r[i]表示以i位置为中心的最长回文串的
半径 -
2.在原字符串的基础上增加占位符,使得长度为n的原字符串变成了一个长度为2n+1的新串,解决了
奇偶的问题
实现
下面结合实例,使用Python来实现Manacher算法
- 1.插入占位符,构造新串
假如给定的字符串是abacca,首先在首位和每个字符中间插入占位符#
# s = 'abacca'
ms = '#' + '#'.join(s) + '#'
# ms = '#a#b#a#c#c#a#'
注意新旧字符串之间的位置对应关系:
a b a c c a
0 1 2 3 4 5
# a # b # a # c # c # a #
0 1 2 3 4 5 6 7 8 9 10 11 12
如果将原串的索引表示为i,新串的索引表示为mi的话,他们的对应关系就是mi = 2i + 1
- 2.半径r的作用
构造一个与新串ms等长的数组r,r[mi]表示以mi位置为中心的最长回文串的半径
所以最终只需要知道最长的半径max(r),以及它对应的位置mi,就可以找到新串ms中的最长回文子串
比如,在给定的例子中,ms的最长回文字串是#a#c#c#a#,对应的mi为8,r[mi]为4
然后就可以根据对应关系找到原串中最长回文串的起始位置start = (mi-r[mi])/2 + 1 = 2,而r[mi]实际上就是原串中最长回文子串的长度(因为在新串ms中引入了占位符之后长度变成2倍了)
因此得到了新串ms的mi之后,最终的答案就是s[start:start+r[mi]-1]
- 3.状态转移方程
因为回文串是对称的,我们可以利用这一点来进行一些判断
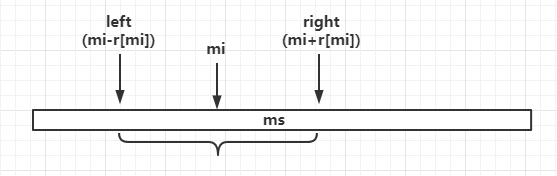
如图所示,用mi表示当前右端点最靠右的回文子串的中心位置(所有的操作都是对ms而言),left与right分别表示表示以mi为中心的回文子串的左右端点
在不断向右遍历ms的过程中,用i表示当前位置,有以下几种情况:
1.i在right左侧(i <= right)
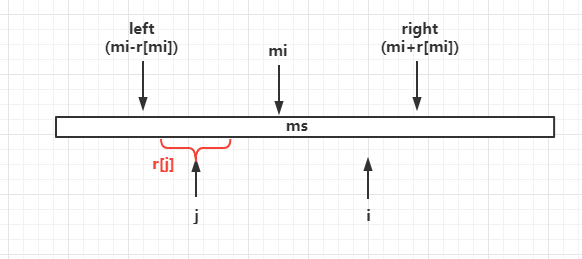
因为i在以mi为中心的回文串内,所以可以找到它的对称点j(j=2*mi-i),而r[j]是已经知道的
这里又分为两种情况:
(1) 以j为中心的回文子串的边界在以mi为中心的回文子串内部,此时r[i]=r[j]
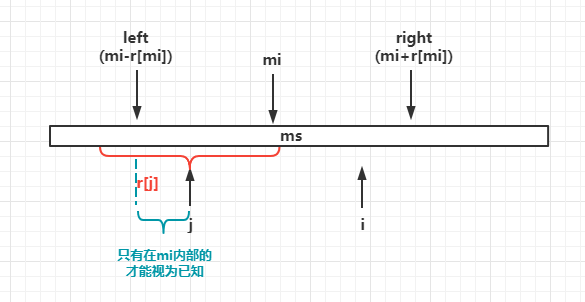
(2)以j为中心的回文子串的边界在以mi为中心的回文子串外部,由于j的外面部分对于i不再适用,所以最多只能让以i为中心的回文子串到达mi的右边界right,即r[i]=right-i
同时因为外部是否是回文串我们不知道,所以要从两个端点逐个向外比较(暴力解法),不过因为有了r[i]的优化,执行暴力解法的次数大大减少
2.i在right右侧(i > right)
因为i不在mi的已知范围内了,这种情况没有办法利用r[i],只能老老实实的使用暴力解法
把这一部分用代码实现一下就是:
l = len(ms)
right = mi + r[mi]
left = mi - r[mi]
j = mi*2 -i
if i <= right:
if j - r[j] > left: # 在mi内部
r[i] = r[j]
else: # 在mi外部
r[i] = right - i
# 暴力解法,向两边扩散
while i + r[i] < l and i - r[i] >= 0 and ms[i+r[i]] == ms[i-r[i]]:
r[i] += 1
else:
r[i] = 1
# 暴力解法,向两边扩散
while i + r[i] < l and i - r[i] >= 0 and ms[i+r[i]] == ms[i-r[i]]:
r[i] += 1
上面的写法有一些冗余,可以稍微优化一下:
l = len(ms)
right = mi + r[mi]
j = mi*2 -i
if i <= right:
r[i] = min(r[j], right-i) # 这里将情况1中的两种子情况合并了一下
else:
r[i] = 1
# 暴力解法,向两边扩散
while i + r[i] < l and i - r[i] >= 0 and ms[i+r[i]] == ms[i-r[i]]:
r[i] += 1
完整代码
def longestPalindrome(s):
if len(s) < 2:
return s
ms = '#' + '#'.join(s) + '#'
l = len(ms)
r = [0] * l
# mi表示当前右端点最靠右的回文子串的中心位置
mi = 0
# ans_i表示最长回文串的中心
ans_i = 0
for i in range(l):
# 核心部分
right = mi + r[mi]
j = mi*2 -i
if i <= right:
r[i] = min(r[j], right-i)
else:
r[i] = 1
while i + r[i] < l and i - r[i] >= 0 and ms[i+r[i]] == ms[i-r[i]]:
r[i] += 1
# 更新mi
if i + r[i] > right:
mi = i
#更新ans_i
if r[ans_i] < r[mi]:
ans_i = mi
start = (ans_i-r[ans_i]) // 2 + 1
return s[start:start+r[ans_i]-1]