使用Go语言实现红黑树
前置知识:二叉搜索树
红黑树是进阶版的二叉搜索树,普通的二叉搜索树在顺序键构造时,复杂度为O(n):
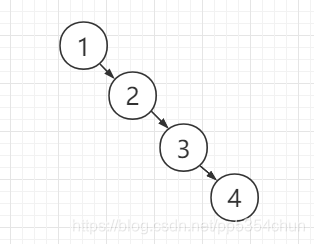
而红黑树则通过为节点额外添加一些属性改善了这一问题,无论以何种顺序构造红黑树,都能得到O(log n)的复杂度
要想学习红黑树,首先需要了解2-3树
2-3树
对于二叉搜索树,每个节点有一个键和两个链接,称这种节点为2-节点,在它的基础0上引入3-节点,它有两个键和三个链接

查找
2-3树的查找操作与二叉搜索树基本一致,只是在3-节点处需要比较的键由一个变成了两个
插入
2-3树的插入操作也与二叉搜索树相似,首先将给定的键在树中查找,如果命中,就更新对应的值,如果未命中则要复杂一些,分为以下几种情况:
向2-节点插入
如果查找未命中结束于一个2-节点,只需要将新键插入到这个2-节点中合并成为一个3-节点
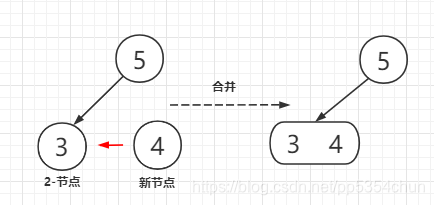
向3-节点插入
如果查找未命中结束于一个3-节点,先将这个新键插入到3-节点中合并为一个临时的4-节点,再将这个4-节点分解为由三个2-节点构成的高度为2的树

向上传递
在向3-节点插入时,如果3-节点有父结点,就要将插入操作向上传递,思想是将新生成的高度为2的子树的根节点作为新的要插入的节点,向它的父结点插入
当父节点是2-节点时:

当父结点是3-节点时:
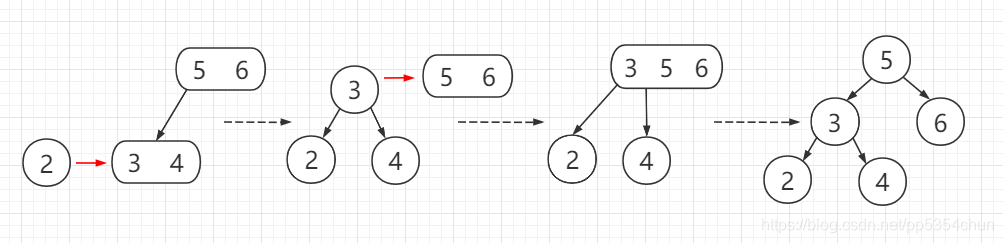
按照这种方式一层一层向上传递,直到根节点
从上面的插入操作可以看出,在2-3树中,当一侧的节点增加时,会将节点合并并向上传递,最终在另一侧生长出节点,这样就保证了树的平衡性(同一根节点的左右子树高度之差不超过1)
所以无论以何种顺序生成2-3树,都不会出现单侧生长的情况,能够得到O(log n)的复杂度
红黑树
2-3树已经满足了平衡性的要求,但是在2-3树中,有的节点有一个键,有的节点有两个键,实际实现起来很不方便
所以红黑树出现了——它将2-3树中的3-节点拆分成了一个根节点和通过红色链接指向的左节点(当然红色右链接也可以,思想是一样的),这种红黑树称为左偏红黑树,在本文中统一称为红黑树(左偏红黑树比普通的红黑树要简单一些,但是思想是相似的,理解了左偏红黑树之后理解普通红黑树会很容易)

所以就有了下面的等价:
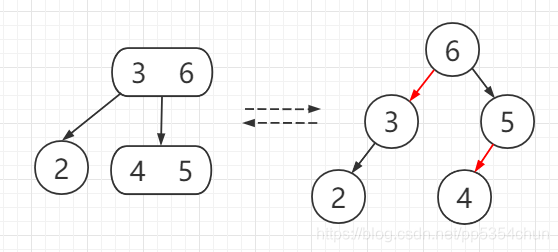
为了表示方便,将红链接指向的节点称为红节点,黑链接指向的节点称为黑节点:
红黑树的性质
通过上面的方法从2-3树转换成的红黑树具有以下性质:
-
1.红节点都是左孩子
-
2.没有连续的红节点
-
3.根节点是黑节点
-
4.黑节点完美平衡:每一条从根节点到叶子节点的路径上黑节点的数量相同
红黑树的属性
相比于二叉搜索树,红黑树的节点仅仅多了一个颜色属性,用true表示红节点,false表示黑节点
var RED bool = true
var BLACK bool = false
type Node struct {
Key int // 用于比较的键
Value int // 该节点存储的值
Left *Node // 左孩子
Right *Node // 右孩子
N int // 以当前节点为根的子树具有的节点数
Color bool // 节点的颜色
}
// 返回以当前节点为根节点子树中节点总数
func (n *Node) size() int {
if n == nil {
return 0
}
return n.N
}
// 检查当前节点是否为红节点,默认空节点为黑色
func (n *Node) isRed() bool {
if n == nil {
return false
}
return n.Color == RED
}
查找
红黑树的查找操作和二叉搜索树完全一致
插入
红黑树的插入操作要复杂一些,因为它要保持红黑树的性质
首先有一个前提:每当插入一个新节点,无论在什么位置,都先将其假定为红节点
插入操作的核心思想是:消除红色右节点与连续的红色左节点
而实现这种思想用到的方法是旋转和变色
插入操作有以下几种情况:
1.向黑色节点的左侧插入(直接)
这是最简单的一种情况,等价于向2-3树的2-节点插入,而且新节点就是左孩子,所以不需要做任何变换
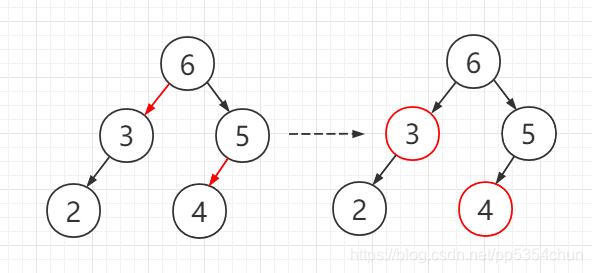
2.向黑色节点的右侧插入,且黑节点的左孩子是黑色(左旋转)
这种情况等价于2-节点的右侧插入,但由于我们定义了红色节点只能是左孩子,而此时出现了红色的右节点,所以通过一次左旋操作来置换黑色父结点和红色右节点
左旋转操作代码实现:
func (n *Node) rotateLeft() *Node {
x := n.Right
n.Right = x.Left
x.Left = n
x.Color = n.Color
n.Color = RED
x.N = n.N // x现在的N是n之前的N
n.N = n.Left.size() + n.Right.size() + 1
return x
}
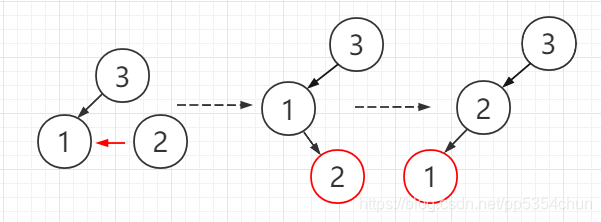
3.向黑色节点的右侧插入,而黑色节点的左孩子是红节点(变色)
这种情况对应于2-3树中向3-节点右侧插入的情况,此时将两个孩子都变为黑色(分解临时4-树),并将父结点变为红色(向上传递)
变色操作代码实现
func (n *Node) flipColorRootRed() {
if n == nil {
return
}
n.Color = RED
n.Left.Color = BLACK
n.Right.Color = BLACK
}
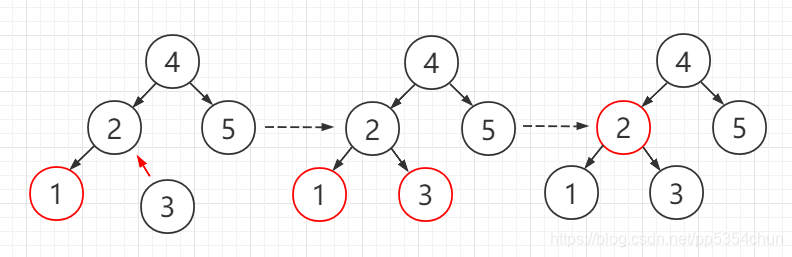
4.向红色节点的左侧插入(右旋转+变色)
这种情况相当于向3-节点左侧插入,此时新子树的根节点应该是中间的节点,所以先向右旋转,变成黑色节点+两个红色孩子的情况,再进行变色操作
右旋转操作代码实现
func (n *Node) rotateRight() *Node {
x := n.Left
n.Left = x.Right
x.Right = n
x.Color = n.Color
n.Color = RED
x.N = n.N
n.N = n.Left.size() + n.Right.size() + 1
return x
}
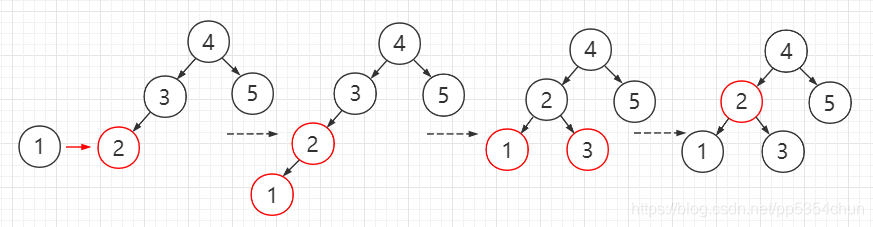
5.向红色节点的右侧插入(左旋转+右旋转+变色)
相当于向3-节点中间插入,此时新子树的根节点应该是新插入的节点,所以先向左旋转,变成黑色节点+两个红色孩子的情况,再进行变色操作
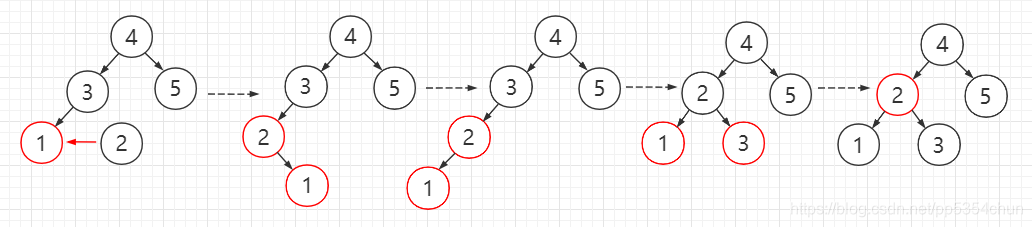
插入操作代码实现
有了以上几种情况的处理,我们就可以实现红黑树的插入操作了
func (n *Node) put(key, value int) *Node {
root := n.putNode(key, value)
root.Color = BLACK // 保证根节点是黑色
return root
}
func (n *Node) putNode(key, value int) *Node {
if n == nil { // 新插入的节点总是假定为红色
return &Node{Key: key, Value: value, Color: RED, N: 1}
}
if key < n.Key {
n.Left = n.Left.putNode(key, value)
} else if key > n.Key {
n.Right = n.Right.putNode(key, value)
} else {
n.Value = value
}
if n.Right.isRed() && !n.Left.isRed() {
n = n.rotateLeft()
}
if n.Left.isRed() && n.Left.Left.isRed() {
n = n.rotateRight()
}
if n.Left.isRed() && n.Right.isRed() {
n.flipColorRootRed()
}
n.N = n.Left.size() + n.Right.size() + 1
return n
}
删除
红黑树的删除操作是最复杂的,因为涉及到大量不同的情况,这一部分结合2-3树更容易理解
删除操作的核心思想是不能删除单独的黑节点(2-3树中的2-节点)
而当要删除的目标就是一个黑节点时,就要从它的父亲或兄弟处借一个节点过来
红黑树的删除分为以下几种情况:
1.删除叶子节点
1.1叶子节点是红节点
这是最简单的情况,因为红节点不影响红黑树的平衡性,红色的叶子节点可以直接删除(相当于在2-3树中删除了叶子3-节点中小的那个键,树的节点数不变,高度也不变)
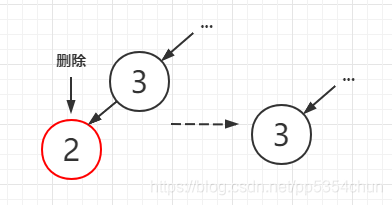
1.2叶子节点是黑节点
如果存在叶子黑节点,则这个叶子节点必然有兄弟(否则不满足黑色平衡),而删除了这个黑色结点之后就不平衡了,所以要向父亲或兄弟借一个节点过来
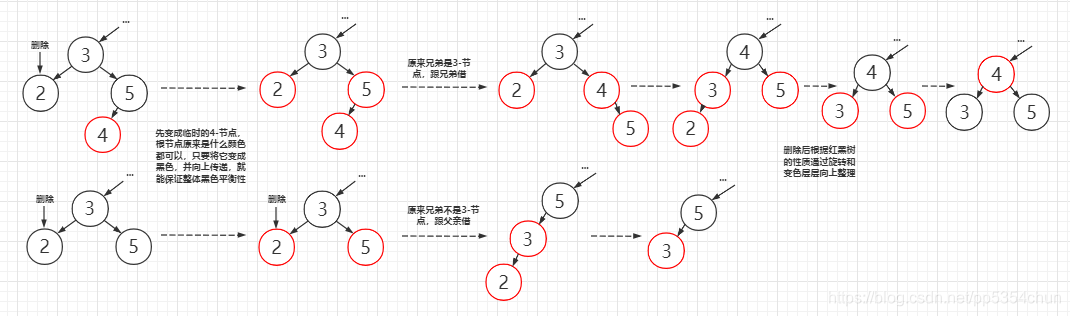
借节点的思想是删除操作的核心,通过它来维持黑色平衡,在删除之后就可以根据上面的旋转和变色操作来进行层层向上的修正
实现代码:
// 将根节点转换成为一个临时4-节点
func (n *Node) flipColorRootBlack() {
if n == nil {
return
}
n.Color = BLACK
n.Left.Color = RED
n.Right.Color = RED
}
// 从右向左借
func (n *Node) moveRedLeft() *Node {
n.flipColorRootBlack() // 先创建一个临时4-节点(默认从父结点借)
if n.Right.Left.isRed() { // 如果兄弟是3-节点,就从兄弟节点里面借
n.Right = n.Right.rotateRight()
n = n.rotateLeft()
}
return n
}
上面图示中是删除左侧的黑节点,所以要从右向左借,如果删除右侧黑节点就需要从左向右借
因为是左偏红黑树,这里左右侧的操作有些不同
// 从左向右借
func (n *Node) moveRedRight() *Node {
n.flipColorRootBlack()
if !n.Left.Left.isRed() { // 说明左边比右边多节点,可以借给右边
n = n.rotateRight()
}
return n
}
2.删除非叶子节点
对于非叶子节点,仍然采用和二叉搜索树一样的思想:用前驱节点或后继节点来替换当前节点
我们在这里仍然选择使用后继节点来替换,后继节点就是右子树中键最小的那个节点
于是问题就转换成了:给定一个节点n,找到它的后继节点(n.Right.min())并复制,删除后继节点(n.Right.deleteMin()),并用后继节点替换当前节点
2.1删除最小键
对于左偏红黑树来说,最小键一定出现在叶子节点,不会存在一个节点只有右子树而没有左子树(违反了黑色平衡性),所以删除最小键最终也就是上面讲的删除叶子节点
而在从根节点走到叶子节点的过程中,有一点需要注意:因为最小键出现在左侧,查找到路线一定是向左下,而每当左侧路径上出现了单独的黑节点(2-节点)时,就像前面删除叶子节点一节中提到的一样,对2-节点的删除会导致黑色不平衡,所以要向兄弟或父亲来借一个节点
每一次出现2-节点都要借,这样才能保证删除后的树还是黑色平衡的
代码实现:
func (n *Node) deleteMin() *Node {
// 这是一层单独对当前根节点的包装(注意当前根节点不一定是整棵树的根节点)
// 如果根节点的左右孩子都不是红节点(在操作过程中可能会产生临时4-节点),
// 意味着当根节点是一个2-节点,它需要向上借节点
if !n.Left.isRed() && !n.Right.isRed() {
n.Color = RED
}
n = n.doDeleteMin()
if n != nil {
n.Color = BLACK
}
return n
}
func (n *Node) doDeleteMin() *Node {
if n.Left == nil {
return nil
}
if !n.Left.isRed() && !n.Left.Left.isRed() {
n = n.moveRedLeft() // 如果左侧是2-节点,就需要从父结点或兄弟节点借
}
n.Left = n.Left.doDeleteMin()
n = n.balance() // 在删除之后,根据红黑树的性质层层向上修正
return n
}
// 与插入操作最后的修正方式一样
func (n *Node) balance() *Node {
if n.Right.isRed() {
n = n.rotateLeft()
}
if n.Left.isRed() && n.Left.Left.isRed() {
n = n.rotateRight()
}
if n.Left.isRed() && n.Right.isRed() {
n.flipColorRootRed()
}
n.N = n.Left.size() + n.Right.size() + 1
return n
}
下面是一个删除最小键的实例,可以帮助理解
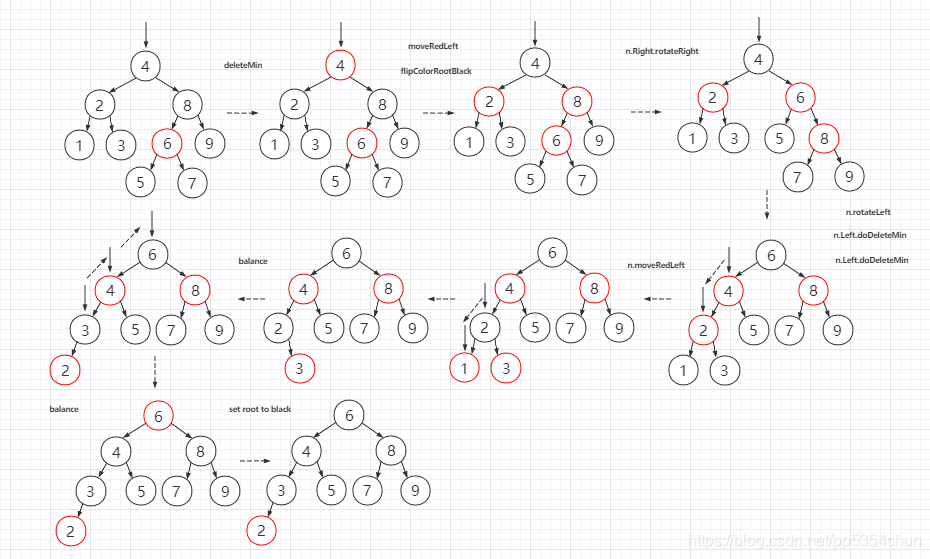
2.2删除节点
实现了删除最小键的方法,整体的删除操作就容易实现了,首先对于当前节点,找到它的后继节点:
func (n *Node) min() *Node {
if n.Left == nil {
return n
}
return n.Left.min()
}
然后复制这个后继节点,并将其删除,然后再替换当前的节点就可以了
代码实现:
func (n *Node) delete(key int) *Node {
// 依然需要对当前根节点进行包装
if !n.Left.isRed() && !n.Right.isRed() {
n.Color = RED
}
n = n.doDelete(key)
if n != nil {
n.Color = BLACK
}
return n
}
func (n *Node) doDelete(key int) *Node {
if key < n.Key {
if !n.Left.isRed() && !n.Left.Left.isRed() { // 左边是2-节点就向父亲或兄弟借一个
n = n.moveRedLeft()
}
n.Left = n.Left.doDelete(key)
} else {
if n.Left.isRed() { // 这个时候要删父结点或右节点,如果当前是一个3-节点,就借它们一个
n = n.rotateRight()
}
if key == n.Key && n.Right == nil {
// 经过前面的操作,此时如果右节点为空,左节点也必为空(否则就不平衡了)
// 当前节点就是一个红色的叶子节点,可以直接删掉
return nil
}
if !n.Right.isRed() && !n.Right.Left.isRed() {
n = n.moveRedRight() // 从左边借一个
}
if key == n.Key { // 用后继节点替换当前节点
t := n.Right.min()
n.Value = t.Value
n.Key = t.Key
n.Right = n.Right.deleteMin()
} else {
n.Right = n.Right.doDelete(key)
}
}
return n.balance()
}
至此,对于红黑树的增删查改操作就全部实现了
总结
-
红黑树的查找操作和二叉搜索树一样
-
对于插入操作,最核心的思想是保证没有红色右节点和连续的红色左节点,在需要时通过旋转和变色来修正
-
对于删除操作,最核心的思想是保证黑色平衡性,不能删除单独的黑节点,在需要时通过向父亲和兄弟借节点来补足,删除后同样需要修正
测试
写个程序来测试一下上面的红黑树代码:
// 按顺序打印键
func (n *Node) print() {
if n == nil {
return
}
n.Left.print()
fmt.Print(n.Key)
n.Right.print()
}
func main() {
nums := []int{1, 2, 3, 4, 5, 6, 7, 8, 9}
root := &Node{Key: nums[0], Value: nums[0], N: 1}
for _, n := range nums[1:] {
root = root.put(n, n*n)
}
root.print()
fmt.Println()
root = root.delete(6)
root.print()
}
输出结果为:
123456789
12345789
也可以自己写个程序打印出每个节点的颜色等属性,以后就可以去跟别人说:我学会红黑树啦!
- 以上算法实现思想来自 《算法第4版》
