Welcome, this is Chunar!
  • Mar 21, 2021

手把手教你实现二叉搜索树——从图示到代码

 

使用Go语言实现二叉搜索树

使用Go语言实现二叉搜索树

二叉搜索树（Binary Search Tree, BST）是一种重要的数据结构，它在随机键构造时能够达到O(log n)的查找与插入复杂度

BST的性质：

BST是一颗二叉树，且对于每一个节点n，它的左子树的键都小于n的键，右子树的键都大于n的键

BST节点的属性

结合上面的性质，为BST的节点维护5个属性：

（本文的所有代码均基于Go编写）

type Node struct {
	Key   int     // 用于比较的键
	Value int     // 该节点存储的值
	Left  *Node   // 左孩子
	Right *Node   // 右孩子
	N     int     // 以当前节点为根的子树具有的节点数
}

Node.N这个属性是为了方便统计节点数量，并不影响BST算法的实现，不过对于N的计算很好的体现了递归的思想

用一个函数size()来包装对Node.N的访问：

func (n *Node) size() int {
	if n == nil {
		return 0
	}
	return n.N
}

查找

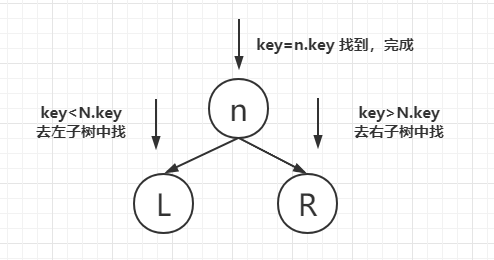
sQ8cnS.png

BST的查找操作比较简单，如果给定的键大于当前节点的键，就向右子树继续查找，小于当前节点的键，就像左子树继续查找，如果最终到了叶子节点还是没有找到，就返回一个默认的错误值：

func (n *Node) get(key int) int {
	if n == nil {
		return -1
	}
	if key < n.Key {
        return n.Left.get(key)
    } else if key > n.Key {
        return n.Right.get(key)
	} else {
		return n.Value
	}
}

插入

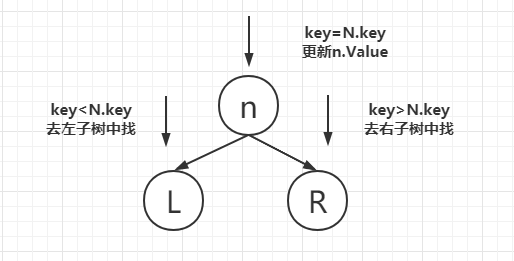
sQ8Dpt.png

对于插入操作，依然按照查找的规律寻找插入位置，如果给定的键已经存在与BST中，则更新它的值，如果不存在，则要在指定的位置新建一个节点，并自下向上更新节点的总数

func (n *Node) put(key int, value int) *Node {
	if n == nil {  // 找到了nil说明给定的key在BST中不存在，为其新建一个节点
		return &Node{Key: key, Value: value, N: 1}
	}
	if key < n.Key {
		n.Left = n.Left.put(key, value)
	} else if key > n.Key {
        n.Right = n.Right.put(key, value)
	} else {
		n.Value = value
    }
    // N的更新发生在递归调用之后，所以会层层向上更新
	n.N = n.Left.size() + n.Right.size() + 1
	return n
}

删除

最简单的删除操作就是删除叶子节点，只需要将当前节点删除（nil），并更新一下相关的父结点中的N属性：

sQGiHe.png

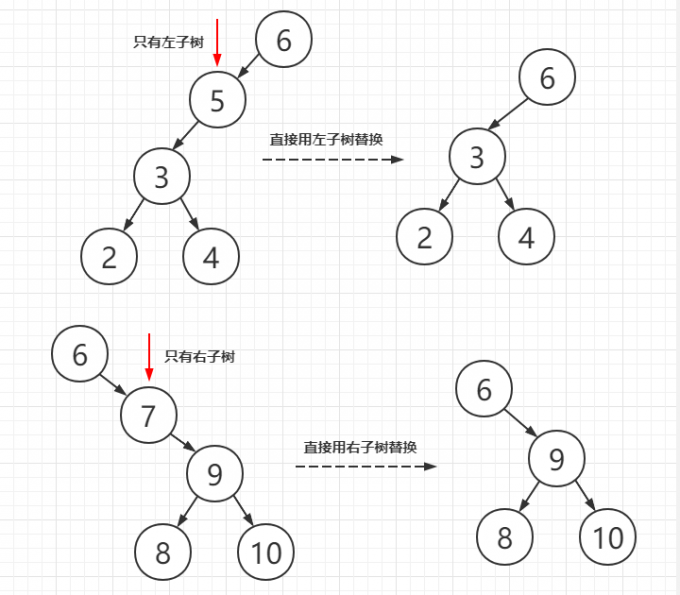
而对于非叶子节点，可能有一个子节点或两个子节点，如果只有一个子树，可以直接用非空的那个子树替换当前节点，此时BST的性质完全保持一致

sQt3Ue.md.png

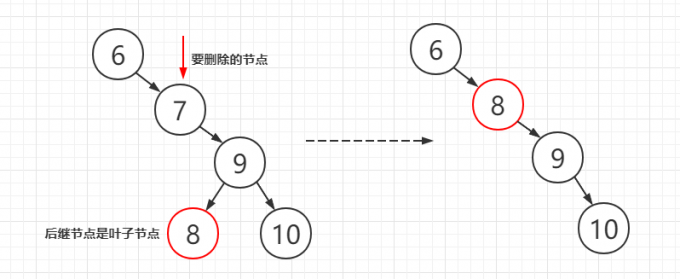
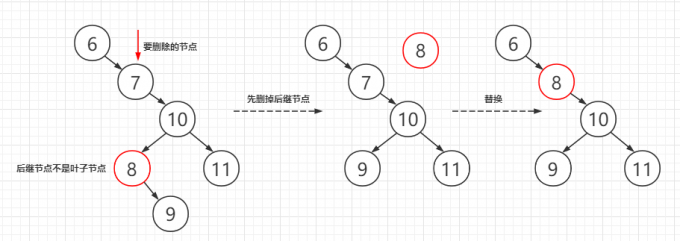
如果有两个子节点，删除的思想是将当前节点替换为它的前驱或后继节点

根据BST的性质，一个节点的前驱节点就是它左子树中的最大节点（左子树中最右面的节点），后继节点就是右子树中的最小节点（右子树中最左面的节点）

可以任选前驱或后继节点进行替换，本文中的实现全部选择后继节点（对于前驱节点，操作方法是对称的）

这里有两种情况：

  • 1.后继节点就是一个叶子节点，可以直接将后继节点从原来的位置删除，并替换到现在的位置

sQtXqK.md.png

  • 2.后继节点不是叶子节点，但它必然没有左孩子，所以按照删除只有一个字节点的方法将其从原来的位置删除，并替换到现在的位置

sQUn0K.md.png

代码实现为：

// 找到以n为根的最小节点
func (n *Node) min() *Node {
	if n.Left == nil {
		return n
	}
	return n.Left.min()
}

// 删除以n为根的最小节点
func (n *Node) deleteMin() *Node {
	if n.Left == nil {
		return n.Right
	}
	n.Left = n.Left.deleteMin()
	n.N = n.Left.size() + n.Right.size() + 1
	return n
}

// 删除节点
func (n *Node) delete(key int) *Node {
	if n == nil {
		return nil
	}
	if key > n.Key {
		n.Right = n.Right.delete(key)
	} else if key < n.Key {
		n.Left = n.Left.delete(key)
	} else {
		if n.Left == nil {
			return n.Right
		}
		if n.Right == nil {
			return n.Left
		}
		t := n
		n = t.Right.min()  // 找到后继节点
		n.Right = t.Right.deleteMin()  // 删除后继节点
		n.Left = t.Left  // 替换
	}
	n.N = n.Left.size() + n.Right.size() + 1
	return n
}

测试

BST的增删查改操作已经全部实现了，用下面的代码测试一下：

// 按顺序输出BST的节点键
func (n *Node) print() {
	if n == nil {
		return
	}
	n.Left.print()
	fmt.Print(n.Key)
	n.Right.print()
}

// 打乱数组顺序
func shuffle(nums []int) []int {
	var ans []int
	for len(nums) > 0 {
		i := rand.Intn(len(nums))
		ans = append(ans, nums[i])
		nums = append(nums[:i], nums[i+1:]...)
	}
	return ans
}

func main() {
	nums := []int{1, 2, 3, 4, 5, 6, 7, 8, 9}
	nums = shuffle(nums)
	fmt.Println(nums)
	root := &Node{Key: nums[0], Value: nums[0], N: 1}
	for _, n := range nums[1:] {
		root = root.put(n, n*n)
    }
    root.print()
	root = root.delete(5)
	root.print()
}
  • 以上算法实现思想来自 《算法第4版》
Search